15 Physical Processes, Field Estimations and Interdisciplinary Ocean Modeling

Allan R. Robinson

Harvard University

Excerpted from Reports in Meteorology and Oceanography 51 Harvard

University

Interdisciplinary Oceanic Forecast Systems

Realistic oceanic interdisciplinary modeling and forecasting involves a coupled physical/biological-chemical or physical/acoustical system. The three major components of the coupled system consist of the dynamical system, the biological-chemical or acoustical system, and the interfacing scheme. Accuracy, efficiency, and sensitivity considerations require significant research efforts for all components of the coupled system. The overall coupled system is quite complex, but its overall parametric dependencies and sensitivities must be determined, qualitatively and quantitatively. For example, what is the sensitivity of biological and chemical results to both the explicit and subgrid scale physical assumptions made in the dynamical forecast model? Aspects of the physical modeling, such as transports at the base of the surface mixed layer, may need more rigorous treatment for ocean biogeochemical/ecosystem (OBCE) model interfacing than for simply advancing the physics. Many of the large number of parameters which characterize the OBCE model are very poorly known. Thus sensitivity analysis plays a critical role in (semi)quantitative estimates of biological and chemical fields and processes.

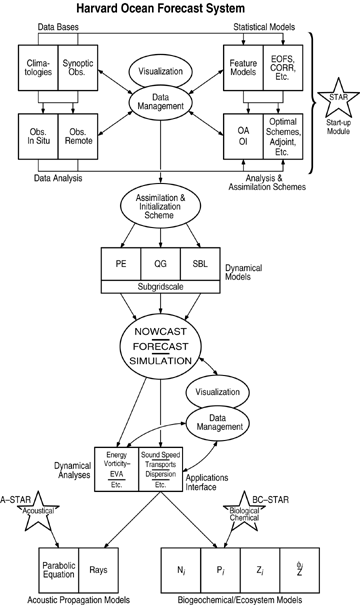
The environmental system for forecasting and simulations has subcomponents which serve various purposes and which consist of: data sets; schemes (algorithms) for data manipulation and assimilation; numerical dynamical model implementations; dynamical analysis schemes and applications models. A schematic flow diagram for the interdisciplinary ocean forecast system developed at Harvard and presently in scientific and operational use is shown in Figure 15.1. The environment in general is characterized: i) by climatological (historical-statistical) data, ii) by a synoptic data base for initialization and updating (assimilation), and iii) by a set of assumptions. For example, large and mesoscale bottom topography can be accurately included directly; whereas, the smaller bottom topographic scales can never be treated in detail and are smoothed or parameterized by a roughness model. Furthermore, the larger topographic scales may be compromised by the representation required by the computational algorithm, such as a step representation (i.e., a discrete depth for each grid location) for input to a dynamical model.

Central to the environmental forecast system of Figure 15.1 is the dynamical model set component which is characterized both by the explicit physics governing the scales of motion resolved by the computational numerical grid and by the smaller subgrid scale (SGS) physical modeling assumptions. The resolved physical scales may be governed by primitive equation or quasigeostrophic model dynamics. Special physics may be introduced near the surface or

Figure 15.1. Schematic of the Modular Harvard Forecast System.

bottom boundary or near coasts. The physics adopted should: be adequate for the representation and evolution of the oceanographic features in the environmental region; filter unwanted phenomena; and lead to simple interpretations of results. The interdisciplinary application may put additional constraints on the representation of the explicit physics of the dynamical model or such requirements may be dealt with in coupling schemes.

Other major components of the environmental system are the statistical model set and the data analyses and management schemes. Any realistic field estimate must be based on synoptic observations which generally today are acquired by an efficient mix of in situ and remote sensors. The data analyses module of Figure 15.1 thus includes software components for the treatment of hydrographic, current meter, float, altimetric, etc. data sets. Data is mapped onto regular grids via (multivariate) objective analysis (OA) schemes which interpolate via the minimization of selected expected error norms. These objective analysis techniques have been extended to biological and chemical data sets. Additionally, statistical model components may include empirical orthogonal functions, in the horizontal or vertical, or other modal representations. Of special note are statistical model representations of typical synoptic structures, the feature models, which are utilized to minimize the observational data requirements necessary to achieve a synoptic realization of the state of the system. Analysis, initialization, and data assimilation schemes meld various types of data with different sampling schemes into estimates of fields of interest, input data into models, and produce melded estimates from observations and dynamical model output. Various methods and techniques, some borrowed from meteorology and engineering, are being explored now in oceanography. The assimilation process may be continuous or at set intervals, and various types of in situ or remotely sensed data may be utilized in combination. The schematic of Figure 15.2 represents a sequential assimilation process.

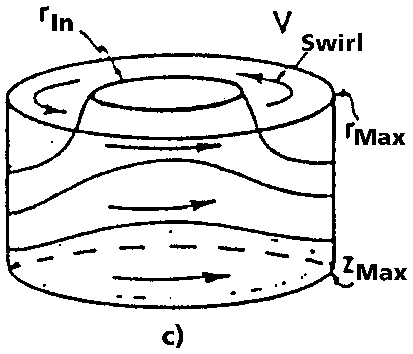
Figure 15.2. JGOFS Spring Bloom Experiment. a) Relative eddy sizes and positions with GEOSAT tracks overlaid; b) GEOSAT altimeter signal along track 122b; c) Eddy feature model.

The Assimilation Initialization Scheme (AIS) module of Figure 15.1 is of particular importance. It may be direct OA data mapping, multiscale feature models, the product of the Fleet Numerical Oceanographic Center (OTIS) (Clancy et al., 1992), etc. The options for data types, processing, and representation afforded by the Harvard ocean forecast system and simulation are sufficiently comprehensive and flexible that the preinitialization/assimilation modules in Figure 15.1 are grouped together into a Start-Up megamodule (STAR). The Physical (P-Star) module is shown explicitly on the figure whereas the equally complex acoustical (A-Star) and biological/chemical (BC-Star) start-up megamodules are only shown symbolically. Assimilation of biological and chemical data should yield important results in the near future. Obtaining efficient, accurate environmental and multidisciplinary field estimates is technically complex, and although the development of relevant schemes, their validation and the establishment of their sensitivities are still at an early stage, such estimates are now available.

The environmentally forecast or simulated physical fields may be used for a variety of purposes. Two postprocessing modules are shown in the Figure 15.1 schematic. The first is a dynamical process module which does energy and vorticity analyses via term by term balances (EVA) in a manner consistently matched to the dynamical model utilized. The second is a multipurpose applications module. This involves the further treatment of the physical fields for operational or interdisciplinary scientific purposes and includes such operations as the calculation of sound speed profiles, transports of nutrients, dispersion, etc. Biological and chemical dynamical process analysis schemes, analogous to the physical EVA, are under development to postprocess the fields resulting from OBCE model forecasts and simulations. Additional application models are also under development, including bio-optical.

The JGOFS 1989 North Atlantic Bloom Experiment

Nowcasts were provided in real time (Robinson et al., 1993) for the JGOFS experiment based on sea surface height information obtained from the Geosat satellite borne radar altimeter. This is depicted in Figure 15.2. The domain was 540 km by 750 km with the pattern of satellite ground tracks spaced about 1.5 degrees longitude apart as shown in Figure 15.2a. Each track was repeated every 17 days. The height variation along an early track that served first to identify two of the three mesoscale cyclonic eddies located in the domain is presented in Figure 15.2b and the location of the "Big" and "Standard" eddies are shown. It is not possible to locate unambiguously the local undisturbed sea level (z=0) height from altimeter data alone (Glenn et al., 1991) and the zero level on Figure 15.2b was set to depict the two cyclones with additional information from some AXBTs which indicated the presence of cold core eddies. The size and location of the three eddies as revealed by successive Geosat passes is also shown in Figure 15.2a. From this information and from past knowledge of eddies in the general area (Kupferman et al., 1986; Le Groupe Tourbillion, 1988), the indices of eddy feature models (radius, depth of the thermocline, maximum sound speed, etc., Figure 15.2c) were evaluated which were used to initialize the QG model. Dynamical adjustment and dynamical interpolation then provide a consistent estimation of the mesoscale fields throughout the domain. This also provides the mesoscale environment for estimation and study of all the physical and related fields in the upper ocean.

In Figure 15.3 is shown the mixed layer depth and pattern of 25 m temperature on day 138. The biological results (McGillicuddy, 1993) are presented on Figure 15.4. The evolution of the physical fields is shown on Figure 15.4 in terms of the vorticity field.

Figure 15.3. a) Wind speed; b) Net surface heat flux; c) The model predicted mixed layer depth with observations superimposed. d) Mixed layer depth (m) and pattern of 25 m temperature (°C) on day 138. Numbers are minimum, maximum and contour interval values.

The eddies first persist, begin to interact and distort. The interaction between the Standard and Small eddies, for example, elongates and then begins to break up Small. These interactions provide the basis for significant nutrient transports into the upper ocean. Year day 115 is near the start of the bloom, 151 at the end of the bloom, and 181 is well into normal summertime conditions. Nutrient enhancement due to original and prior doming of the isopycnal and isonutrient surfaces in the cyclonic eddies is apparent in the nitrate initial condition on day 115; the phytoplankton is uniform and low at the end of the winter. The vertical velocity of the feature-model initialization is zero. Between days 115 and 151, a bloom occurs that removes nearly all of the nitrate from the mixed layer. The phytoplankton biomass distribution reflects the initial nitrate distribution in that the enhanced nitrate within the eddies has allowed the bloom to proceed much further there. Note the eddy-eddy interactions as shown in the vorticity field. Particularly, the small eddy has interacted vigorously with the standard eddy resulting in transport processes which have significantly increased the nutrient concentration in the center of the small eddy via entrapment. Between days 151 and 180, the increased nutrient in the center of the small eddy gives rise to a local maximum in phytoplankton biomass. The continued eddy-eddy interactions have now produced a nutrient enhancement within the standard eddy which is an order of magnitude greater than the background concentration outside of the eddies. The nutrient transports due to eddy-eddy interactions are in this case much larger than the submesoscale enhancements previously hypothesized to be the most important biological effects of mesoscale motions (Woods, 1988).

Figure 15.4. Temporal development of physical and biological fields. Day 115 is prebloom, 151 is end of bloom and 180 is postbloom. See McGillicuddy (1993) for details.